Как да решим системите на уравненията?
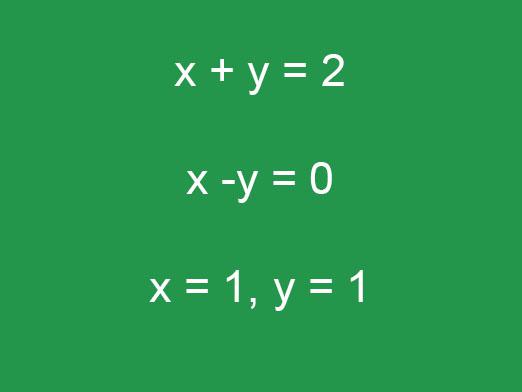
Системата от уравнения - на пръв поглед абсолютнобезполезно и ненужно нещо в живота. Но ако човек се вгледа в същността на процесите, които се случват около нас, в природата, в постиженията на науката и технологиите, става ясно - това не е така. Почти всеки феномен може да бъде описан от система от уравнения, започвайки от дъжд през пролетта, завършвайки с полетите на астероиди в космоса. И както е добре известно, може да се предвиди явление, за което е определено достатъчно точно описание.
Какво представлява система от уравнения
Системата е обикновенауравнения, които трябва да бъдат изпълнени едновременно. На буквата системата е обозначена със скоба от лявата страна, съчетаваща всички уравнения. И как да се реши системата от уравнения? Поради факта, че всички уравнения на всяка дадена система трябва да бъдат в сила заедно, се откриват няколко метода, за да се интерпретира, да се трансформира системата, без да се променят нейните корени. Такива трансформации се считат за еквивалентни. Например, има система "x + y = 2; x - y = 0. "Очевидно е, че нейните корени са х = 1; y = 1 ". Нека да разгледаме еквивалентни трансформации.
допълнение
Решаването на системата от уравнения чрез метода на добавяне е по-лесновсички. Добавяме второто уравнение към първото уравнение и напълно - както лявата, така и дясната част. Получаваме системата "2 * x + 0 * y = 2 + 0; х - у = 0 ". В първото уравнение на системата намираме корен x = 1. Заместим го във второто уравнение и получим стойността на втората променлива y = 1. Системата е решена. Трябва да се помни, че преди добавянето, уравнението може да бъде напълно умножено с константа, която също е еквивалентна трансформация. И тази константа не трябва да бъде положителна.
заместване
Ако задачата звучи като "решаване на систематауравнения чрез метода на заместване "- всичко това е по-лошо. Методът на заместване е по-гъвкав от метода на добавяне, а не един единствен лист може да отиде в една малка система. За да се реши система от уравнения чрез заместване, е необходимо да се вземе едно от уравненията (за удобство - първият) и да го изрази от една от променливите (за удобство, първият отново). Уравнението на формата "х = 2y + 7z + 9a 2Ь - 11" Сега във всички други уравнения, избрани за х го заместят израз «2Y на + 7z + 9a 2Ь - 11", като не забравяме да го умножете по числен коефициент з първоначалното уравнение. Получаваме уравнение, изразяващо x и няколко уравнения от x, които не зависят. След това изпълняваме подобна операция за всички променливи. В последното уравнение последната променлива ще бъде ясно изразена, това е характеристиката на този метод. И вследствие на това може да се намери. Знаейки, последната променлива, е възможно да се замени цифровата стойност в предпоследния уравнението и да намерят вече предпоследния променлива. Продължавайки тези машинации, можете да намерите всички променливи. При решаването на задачите за такъв метод трябва да бъдат много внимателни - това масата на аритметични операции е трудно да се избегне объркване и да се предотврати досадни грешки. За да проверите верността на решението, можете да използвате услугата Wolfram Alpha. Той е мощен компютър център, който може да отговори на най-различни искания, трябва само да се опише проблема, така че да реализира компютъра. Например, за да го попитам система от уравнения, че е необходимо да въведете уравнението, като ги разделяте с точка и запетая.