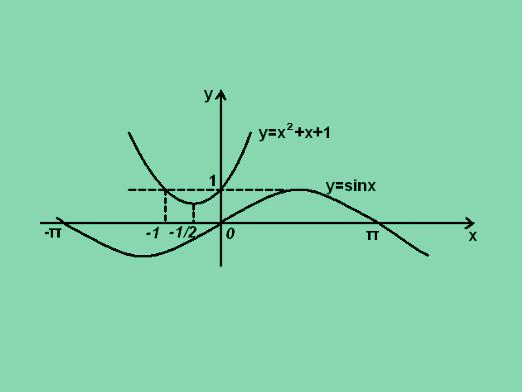
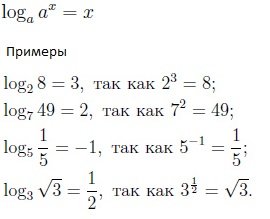Как да решим логаритмични уравнения?

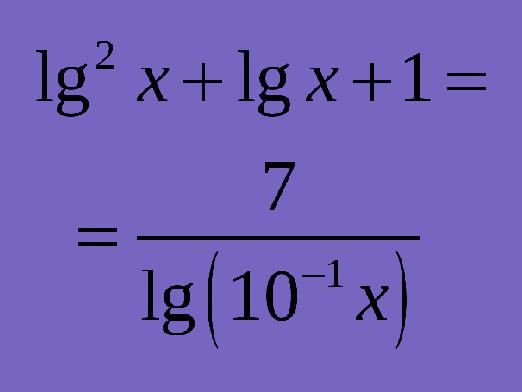
Всеки знае защо ви е необходима математика. Много хора обаче се нуждаят от помощ при решаването на математически проблеми и уравнения. Преди да ви кажа как да се реши логаритмични уравнения, трябва да се разбере какви са те. Уравнения, които съдържат неизвестно в основата на логаритъма или под знака си се наричат логаритмични уравнения. Уравнението на формата: logaX = б, или тези, които могат да бъдат намалени до форма счита за прости логаритмични уравнения.

Правилното решение

За правилното решение на тези уравнения е необходимо да се запомнят свойствата на всяка логаритмична функция:

набор от реални числа (диапазон от стойности)
набор от положителни числа (домейн от определението)
в случая, когато "а" е по-голямо от 1, се получава стриктно увеличаваща се логаритмична функция, ако е по-малка, намалението
с дадените параметри: лога "a" е равна на 1, а лога 1 е равна на нула, е необходимо да се има предвид, че "a" няма да бъде равна на 1 и ще бъде по-голяма от 0.

Правилното решение на логаритмичните уравнениядиректно зависи от разбирането на самия логаритъм. Да вземем пример: 5x = 11. X е номер, на който искате да се издигне 5 до получаване 11. Това число се нарича логаритъма при основа 11 на 5 и е писано в следния вид: х = log511. По този начин, ние успяхме да решим експоненциално уравнение: 5х = 11, получи отговор: х = log511.

Логаритмични уравнения

Уравнение, което има логаритми, се наричалогаритмични уравнения. В това уравнение неизвестни променливи, както и изрази с тях, се намират вътре в самите логаритми. И никъде другаде! Примери за логаритмични уравнения са log2x = 16, log5 (x3-7) = log5 (3х), lg3 (х + 3) + 20 = 15lg (х + 5) и т.н. Не забравяйте, че различни изрази с x-m могат да бъдат само в даден логаритъм.

Ние се отърваваме от логаритмите

Методи за решаване на логаритмични уравнениясе прилагат в съответствие със съществуващата задача, а процесът на вземане на решения като цяло е много трудна задача. Нека да започнем с елементарните уравнения. Най-простите логаритмични уравнения имат следната форма:

logx-21 = 11
log5 (70х-1) = 2
log5x = 25

Решението на логаритмичното уравнение предполагапреход от уравнение с логаритми към уравнение, в което те не съществуват. И в най-простите уравнения това може да се направи в една стъпка. Поради тази причина те се наричат протозои. Например, трябва да решим следното уравнение: log5x = log52. За това нямаме нужда от специални знания. В този пример трябва да се отървем от логаритмите, които развалят цялата картина. Отстраняваме логаритмите и получаваме: x = 2. По този начин, в бъдеще е необходимо да се премахнат ненужните логаритми, ако е възможно. В края на краищата тази последователност позволява да се решат логаритмичните неравенства и уравнения. В математиката тези действия обикновено се наричат потенциализация. Но такова унищожаване от логаритмите има свои собствени правила. Ако логаритмите нямат коефициенти (т.е. са дадени от самите тях), а също и със същата цифрова база, логаритмите могат да бъдат премахнати.

Не забравяйте, че след като премахнем логаритмите, имаме опростено уравнение. Да вземем още един пример:

log9 (5х-4) -log9х. Потентируем и получаваме:

5х-4 = х
5х = х + 4
4х = 4
х = 1

Както виждаме, изтриването на логаритмите, имаме обичайнотоуравнение, което вече трудно може да бъде решено. Сега можете да отидете на по-сложни примери: log9 (60x-1) = 2. Трябва да се позовем на логаритъма (числото, в което е изградена основата, в нашия случай 9), за да получим логаритмичен израз (60х-1). Нашият логаритъм е 2. Оттук: 92 = 60х-1. Логаритъмът вече не съществува. Разрешаваме полученото уравнение: 60x-1 = 59, x = 1.

Този пример решихме според значениетологаритъма. Трябва да се отбележи, че от който и да е номер може да се направи логаритъм, който се изисква. Този метод е много полезен при решаването на неравенствата и логаритмичните уравнения. Ако трябва да намерите корен в уравнението, нека разгледаме как може да бъде направено: log5 (18 - x) = log55

Ако в нашето уравнение двете страни на уравнениетоима логаритми със същата основа, тогава можем да пресметнем изразите, които стоят под знаците на нашите логаритми. Премахваме общата база: log5. Получаваме едно просто уравнение: 18-x = 5, x = 13.

Всъщност, за да реши логаритмичните уравненияне е толкова трудно. Дори и да се има предвид факта, че свойствата на логаритмичните уравнения могат да се различават съществено, все пак няма никакви неразрешими задачи. Необходимо е да знаете свойствата на самия логаритъм, както и да можете да ги прилагате правилно. Не бързайте: запомнете горните инструкции и продължете да решите задачите. В никакъв случай не трябва да се страхувате от сложно уравнение, имате всички необходими знания и ресурси, за да можете лесно да се справите с някоя от тях.

Прочетете повече: