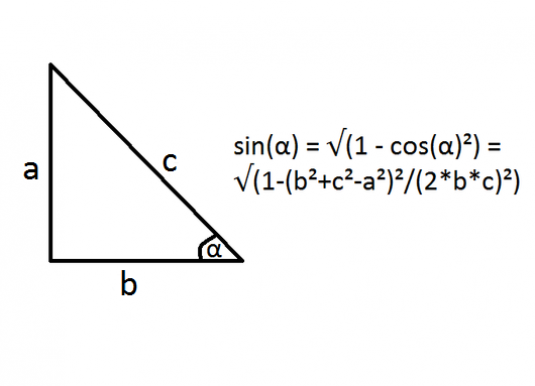Как да си намерим задължително?

Проучването на геометрията помага да се развие мисленето. Този предмет задължително влиза в училищната подготовка. В живота, познаването на тази тема може да бъде полезно - например при планирането на апартамент.

От историята

В рамките на курса на геометрията се изследва и тригонометрията, която изследва тригонометричните функции. В тригонометрията изследваме синуси, косинуси, тангентове и котангенти от ъгъл.

Но за момента ще започнем с най-простите - задължителните. Да разгледаме по-подробно първата идея - синусоида на ъгъла в геометрията. Какво е задължително и как да го намерите?

Понятието "синусов ъгъл" и синусоидите

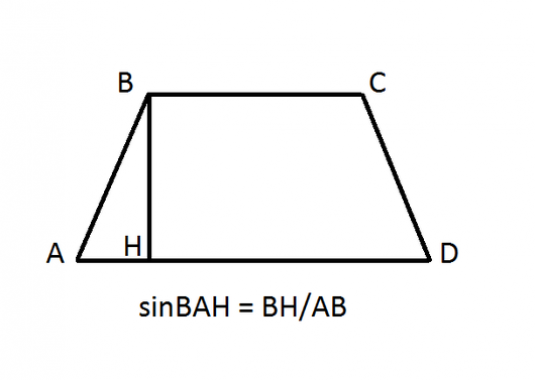
Синусът на ъгъла е съотношението на стойноститепротивоположния крак и хипотенузата на правоъгълен триъгълник. Това е пряка тригонометрична функция, която в буквата е означена като "грях (х)", където (х) е ъгълът на триъгълника.

На графиката синусите на ъгъла се означават от синусоида ωнеговите характеристики. Синусовата вълна изглежда като непрекъсната вълнообразна линия, която се намира в определена рамка на координатната равнина. Функцията е странна, затова е симетрична около 0 в координатната равнина (оставя началото на координатната препратка).

Домейнът за дефиниране на тази функция се намира вварира от -1 до +1 на декартовата координатна система. Периодът на функцията на ъгловия ъгъл е 2 Pi. Това означава, че всеки 2 Pi модел се повтаря и синусоидалната вълна минава през пълен цикъл.

Уравнение на синусоида

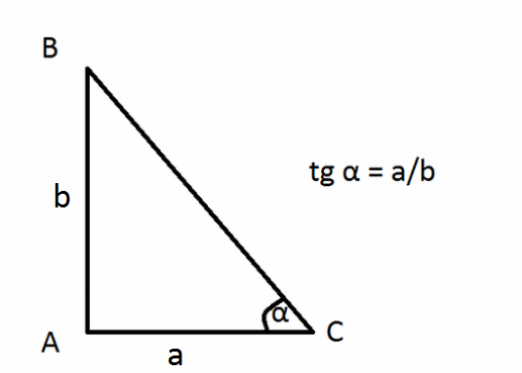
• грях x = a / c
• където а е катетката, противоположна на ъгъла на триъгълника
• в - хипотенузата на триъгълник с прави ъгъл

Ъглови синусови свойства

1. грях (х) = - грях (х). Тази функция показва, че функцията е симетрична и ако зададем стойностите на х и (-x) от двете страни на координатната система, тогава ординатите на тези точки ще бъдат противоположни. Те ще бъдат еднакво един от друг.
2. Друга особеност на тази функция е,че графиката на функцията се увеличава на интервала [-Π / 2 + 2 Пn]; [П / 2 + 2Пn], където п е всяко цяло число. Разсипването на синуса на ъгъла ще се наблюдава на сегмента: [П / 2 + 2 Пn]; [3P / 2 + 2Pn].
3. sin (x)> 0, когато x е в диапазона (2πn, π + 2πn)
4. (х) <0, когато х е в обхвата (-П + 2Пn, 2Пn)

Стойностите на синусите на ъгъла се определят със специалнимаси. Такива таблици са създадени, за да улеснят изчисляването на сложни формули и уравнения. Той е лесен за използване и съдържа не само функции sin (x), но и стойности на други функции.

Освен това, таблицата със стандартните стойности на тези стойностифункциите е включена в изследването за задължителна памет като таблица за умножение. Това важи особено за класовете с физически и математически пристрастия. В таблицата можете да видите стойностите на основните ъгли, използвани в тригонометрията: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 и 360 градуса.

стойност на ъгъла α (градуси)	0	15	30	45	60	75	90	120	135	150	180	270	360
Стойността на ъгъла α в радиани (по отношение на броя pi)	0	π / 12	π / 6	π / 4	π / 3	5π / 12	π / 2	2π / 3	3π / 4	5π / 6	π	3π / 2	2π
грях (задължително)	0	√3-1 / 2√2	1/2	√2 / 2	√3 / 2	√3 + 1 / 2√2	1	√3 / 2	√2 / 2	1/2	0	-1	0

Има и таблица, която определя стойноститетригонометрични функции на нестандартни ъгли. Използвайки различни таблици, можете лесно да изчислите синусите, косинуса, допирателната и котангента от някои ъгли.

С тригонометричните функции се компилиратЕкв. Лесно е да се решат тези уравнения, ако знаем прости тригонометрични идентичности и редукционни функции, например като грях (n / 2 + x) = cos (x) и други. За такива призраци е съставена и отделна таблица.

Как да намерите синусите на ъгъла

Когато задачата е да открием синусите на ъгъла и при условие, имаме само косинус, допирателна или котангента на ъгъла, можем лесно да изчислим желаното с помощта на тригонометрични идентичности.

• грях²x + cos²х = 1

Въз основа на това уравнение можем да открием синусоида и косинуса, в зависимост от това, коя стойност е неизвестна. Получаваме тригонометрично уравнение с една неизвестна:

• грях²х = 1 - cos²х
• sin x = ± √ 1 - cos²х
• CTG²x + 1 = 1 / sin²х

От това уравнение можете да намерите стойността на синуса, като знаете стойността на ъгъла на котангента. За простота заместете греха²x = y, а след това получавате просто уравнение. Например стойността на котангента е 1, след това:

• 1 + 1 = 1 / г
• 2 = 1 / у
• 2y = 1
• y = 1/2

Сега изпълнете обратната подмяна на играта:

• грях²х = 1/2
• грях x = 1 / √2

Тъй като взехме котангента за стандартен ъгъл (45⁰), получените стойности могат да бъдат проверени от таблицата.

Ако ти е дадена стойността на тангента и трябва да намериш задължително, друга тригонометрична идентичност ще помогне:

• tg x * ctg х = 1

От това следва, че:

• ctg х = 1 / tg х

За да откриете синус на нестандартен ъгъл, например 240⁰, е необходимо да се използват формулите за намаляване на ъглите. Знаем, че π съответства на 180⁰, По този начин изразяваме равенството си чрез стандартни ъгли чрез разлагане.

• 240⁰ = 180⁰ + 60⁰

Трябва да намерим следното: грях (180⁰ + 60⁰). При тригонометрията има формули за намаляване, които в този случай са полезни. Това е формулата:

• грях (π + х) = - грях (х)

По този начин синусът на ъгъла от 240 градуса е равен на:

• грях (180⁰ + 60⁰) = - грях (60⁰) = - √3 / 2

В нашия случай, x = 60, и P, съответно, 180 градуса. Стойността (-√3 / 2), която намерихме от таблицата на стойностите на функциите на стандартни ъгли.

По този начин могат да се разширят нестандартни ъгли, например: 210 = 180 + 30.

В учебниците и в Интернет можете да срещнете многоформули за изчисляване на тригонометрични уравнения - изваждане, добавяне, продукция и разделяне на тригонометрични функции на различни ъгли един към друг, възход към властта и преобразуване на една функция в друга с помощта на прости идентичности и много други операции.

За повече информация относно сини и косинуси вижте:

• Какво е задължително
• Как да намерите задължително, ако косинусът е известен