Как да намерим генератора на конус?

Днес ще ви разкажем как да намерите генериращия конус, който често се изисква в училищните проблеми по геометрията.

Концепцията за генератор на конус

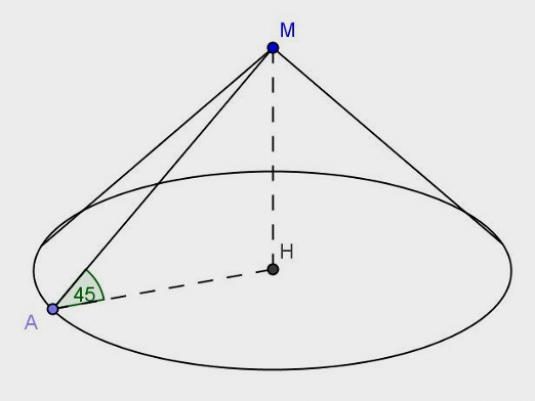
Правият конус е цифрата, която се получава вРезултатът е въртенето на десния триъгълник около единия от краката му. Основата на конуса оформя кръг. Вертикалната секция на конуса е триъгълник, хоризонталата е кръг. Височината на конуса е сегментът, свързващ върха на конуса с центъра на основата. Формиращият конус е сегментът, който свързва върха на конуса с всяка точка от линията на окръжността на основата.

Тъй като конусът се формира от въртенето на правоъгълниктриъгълник, се оказва, че първият крак на такъв триъгълник е височината, вторият е радиусът на кръга, лежащ в основата, а хипотенузата е генераторът на конуса. Не е трудно да се предположи, че питагорейската теорема е полезна за изчисляване на дължината на генератора. И сега повече за това как да намерите дължината на генериращия конус.

Намираме генератора

Най-лесният начин да разберете как да намерите генератор е чрез конкретен пример. Поемат условия са такива проблеми :. височина 9 cm, е необходима база диаметър кръг от 18 cm за намиране на генератор ..

Така че, височината на конуса (9 см.) е един от краката на триъгълник с прави ъгъл, по който се образува този конус. Вторият крак ще бъде радиусът на основния кръг. Радиусът е половината от диаметъра. По този начин разделете диаметъра, който ни е даден наполовина, и получете дължината на радиуса: 18: 2 = 9. Радиусът е 9.

Сега е много лесно да се намери генериращ конус. Тъй като е хипотенузата, а след това на площада от неговата дължина е равна на сумата от квадратите на краката, което означава, че сумата от квадратите на радиуса и височината. Така, образуващи квадрат на дължина = 64 (квадратен дължина радиус) на + 64 (височината на квадрат дължина) = 64x2 = 128. Сега извличане на корен квадратен от 128. В резултат, ние получаваме осем основата на две. Това ще бъде генераторът на конуса.

Както можете да видите, нищо не е сложно в това. Например, взехме простите условия на проблема, но в училищния курс те могат да бъдат по-трудни. Не забравяйте, че за да изчислите дължината на генератора, трябва да разберете радиуса на окръжността и височината на конуса. Познавайки тези данни, лесно е да се намери дължината на генератора.